About the Project

The Procedural Art Generator is an interactive web application that lets you explore and create beautiful mathematical artwork through various procedural generation algorithms. Each algorithm represents different approaches to computer-generated art, from simple particle systems to complex mathematical models like fractals, Voronoi diagrams, and chaotic attractors.

This project was created to showcase the beauty of algorithmic art and provide an accessible way for anyone to experiment with these fascinating mathematical patterns without requiring programming knowledge.

The Algorithms

Particle System

Particle systems simulate the behavior of numerous small particles that follow physical rules. Introduced in the early 1980s by William Reeves at Lucasfilm for the "Genesis Effect" in Star Trek II: The Wrath of Khan, particle systems have become foundational to computer graphics and generative art.

Each particle has properties like position, velocity, size, and lifespan. By simulating thousands of these particles simultaneously, complex emergent patterns can form, creating visually stunning effects like fire, smoke, water, and abstract artistic patterns.

Reeves, W. T. (1983). Particle Systems—A Technique for Modeling a Class of Fuzzy Objects. ACM Transactions on Graphics

Recursive Patterns (Fractals)

Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Fractals were popularized by mathematician Benoit Mandelbrot in the 1970s.

Our implementation uses recursive branching patterns inspired by L-systems (developed by botanist Aristid Lindenmayer in 1968) to create tree-like structures where each branch subdivides into smaller branches, creating complex organic shapes that mimic natural forms like trees, ferns, and coral.

Mandelbrot, B. B. (1982). The Fractal Geometry of Nature

Flow Field

Flow fields (also known as vector fields) represent directional forces across a space. Popularized in generative art by artists like Robert Hodgin and creative coders like Daniel Shiffman, flow fields create mesmerizing flowing patterns.

Our implementation uses Perlin noise to generate smooth, natural-looking vector fields. Particles then traverse these fields, creating flowing lines that reveal the underlying structure of the field. This technique produces organic, river-like patterns that suggest natural flowing systems like water currents, wind patterns, or magnetic fields.

Shiffman, D. (2012). The Nature of Code: Simulating Natural Systems with Processing

Voronoi Diagram

Voronoi diagrams partition space into regions based on distance to a specified set of points. Named after mathematician Georgy Voronoi who formalized them in 1908, these diagrams occur naturally in many contexts, from cell structures to animal territories.

In our implementation, seed points are distributed across the canvas, and each pixel is colored based on which seed point it's closest to. The boundaries between these regions form the characteristic cell-like pattern. Voronoi diagrams can be found throughout nature – from the patterns on a giraffe's coat to the structure of cells in living tissue.

Aurenhammer, F. (1991). Voronoi diagrams—a survey of a fundamental geometric data structure

Wave Patterns

Wave patterns simulate various wave phenomena found in physics, including water waves, sound waves, and electromagnetic waves. Wave mathematics has been studied since ancient times, with modern wave equations formalized by d'Alembert, Euler, and others in the 18th century.

Our implementation combines sine waves of different frequencies, amplitudes, and phases to create complex wave interference patterns. The algorithm can produce a wide range of effects from calm, regular waves to turbulent, chaotic patterns reminiscent of ocean surfaces or sound visualizations.

Strogatz, S. H. (1994). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering

Truchet Tiles

Truchet tiles are a set of decorative patterns created by placing specific designs on square tiles and arranging them on a grid. Named after Sébastien Truchet, a French Dominican priest who studied these patterns in the early 18th century.

Our implementation creates patterns by placing tiles that contain simple geometric elements (like quarter circles or diagonal lines) and rotating them randomly. Despite the simplicity of the individual tiles, complex global patterns emerge when they're combined. This demonstrates how complex, interesting designs can arise from very simple local rules.

Smith, C. S. (1987). The tiling patterns of Sebastien Truchet and the topology of structural hierarchy

Perlin Noise

Perlin Noise is a type of gradient noise developed by Ken Perlin in 1983 while working on visual effects for the film "Tron." He later received an Academy Award for this work. Unlike random noise, Perlin noise creates smooth, natural-looking variations.

Our implementation visualizes Perlin noise directly as a gradient field, where each pixel's color is determined by the noise value at that position. This creates organic, cloud-like patterns that can be used to simulate natural textures like terrain, clouds, marble, fire, and water. Perlin noise is foundational to procedural texture generation in computer graphics.

Perlin, K. (1985). An image synthesizer. ACM SIGGRAPH Computer Graphics

Fractal Brownian Motion (fBm)

Fractal Brownian Motion (fBm) extends Perlin noise by combining multiple layers (octaves) of noise at different frequencies and amplitudes. The concept was formalized in the context of computer graphics by Mandelbrot and Van Ness in 1968, building on work by mathematician Norbert Wiener.

Our implementation layers multiple Perlin noise functions with progressively higher frequencies and lower amplitudes. This creates rich, detailed patterns with both large-scale structure and fine details. fBm is especially useful for creating realistic terrain, clouds, and other natural phenomena that exhibit self-similarity across different scales.

Mandelbrot, B. B., & Van Ness, J. W. (1968). Fractional Brownian motions, fractional noises and applications

L-System

Lindenmayer systems (L-systems) are a type of formal grammar used to model the growth processes of plant development. They were introduced by Hungarian biologist Aristid Lindenmayer in 1968 as a mathematical theory of plant development.

Our implementation uses L-systems to generate fractal-like structures by repeatedly applying rewriting rules to an initial string (axiom), then interpreting the resulting string as drawing commands for a turtle graphics system. This can create complex branching structures like plants, trees, and other organic forms, as well as abstract fractals like the Sierpinski triangle and Koch curve.

Prusinkiewicz, P., & Lindenmayer, A. (1990). The Algorithmic Beauty of Plants

Reaction-Diffusion

Reaction-diffusion systems are mathematical models that describe how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reactions and diffusion. Pioneered by Alan Turing in 1952 in his paper "The Chemical Basis of Morphogenesis."

Our implementation uses the Gray-Scott model, which simulates the interaction between two virtual chemicals. Through the processes of reaction and diffusion, complex patterns emerge over time, including spots, stripes, waves, and maze-like structures. These patterns are remarkably similar to those found in nature, such as animal coat patterns, fingerprints, and coral formations.

Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society B

Penrose Tiling

Penrose tilings are non-periodic tilings discovered by mathematician and physicist Roger Penrose in the 1970s. Unlike regular tilings, Penrose tilings never repeat exactly, yet exhibit stunning fivefold rotational symmetry.

Our implementation uses the kite and dart version of Penrose tiling, where two different rhombus shapes are arranged according to specific matching rules. The resulting patterns have fascinating mathematical properties: they are aperiodic (never repeating), self-similar (containing copies of themselves at smaller scales), and have the golden ratio embedded throughout their structure.

Penrose, R. (1974). The role of aesthetics in pure and applied mathematical research

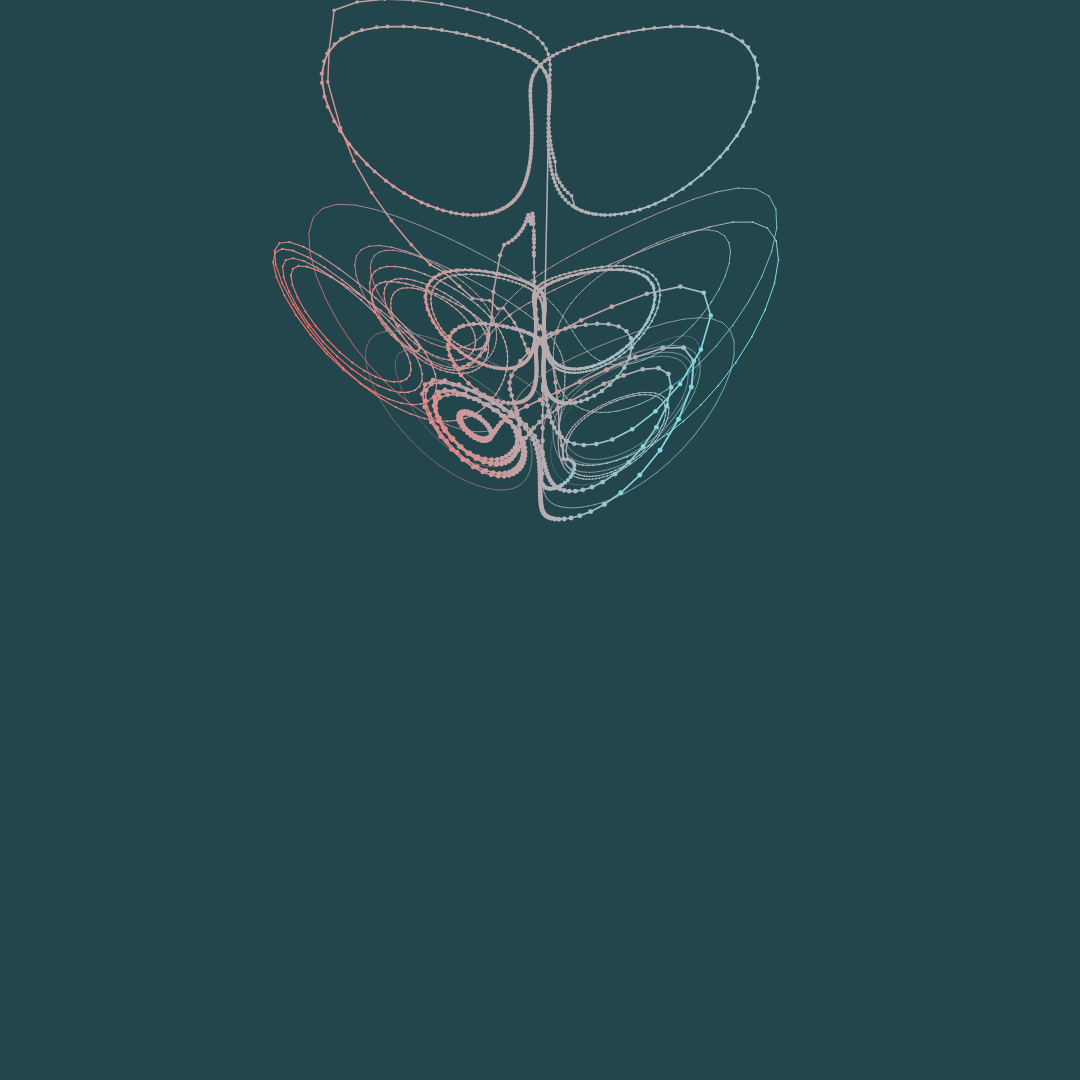
Lorenz Attractor

The Lorenz attractor is a set of chaotic solutions to the Lorenz system of ordinary differential equations. First studied by Edward Lorenz in 1963, it is one of the most famous examples of chaos theory and the "butterfly effect" – the idea that small changes in initial conditions can lead to vastly different outcomes.

Our implementation numerically solves the Lorenz differential equations and visualizes the resulting trajectory. The characteristic butterfly-shaped attractor emerges from this seemingly simple system. Despite being deterministic, the system is highly sensitive to initial conditions, demonstrating the fundamental unpredictability of chaotic systems.

Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences